5 R, JAGS, and RJAGS

Warning: This page contains a lot of HTML graphs that can be slow to load!

From the report introduction:

There are two advantages to our proposed system compared with the current workflow:

1. Our system combines data from multiple sources into a statistical model that includes uncertainty using Bayesian statistics.
2. The operator can interact with the internal model through Excel to conduct scenario analysis and automatically visualise the results.

— Me

This Rmarkdown-generated page will serve as proof that a fully automated proof of concept has been developed. Whether the code is sufficiently commented or not … is a different question.

5.1 Setup

configpath = '../wairakei_data/config.xlsx'
regdatapath = '../wairakei_data/data.xlsx'
extraliqregpath = "../wairakei_data/extra_liq.csv" # for regression
extradatapath = "../wairakei_data/well_pi.csv"     # ts data
pipath <- "../wairakei_data/short version Generation Projection 2016.xlsx"

base_year = '2000'
prediction_date = '2017-12-01'
production_curve_wells = c('wk255', 'wk263')
tsplotwells = c("wk118", "wk216", "wk605")
decline_wells = c(production_curve_wells, "wk272", "wk86", "wk116")
base_datetime = as.POSIXct(paste(base_year, 1, 1, sep='-'))
today_datetime = as.POSIXct(prediction_date)
# theme_update(text=element_text(family="Times New Roman"))
'%ni%' <- Negate('%in%')
# for over-plotting
special_wells = c(production_curve_wells, tsplotwells, "wk86", "wk116")
use.censor = T

n_steps = 1000

censor = function(x, type) {
  # Hash the facility identifier (beware of hash clashes)
  if (!use.censor) {
    return(x)
  } else if (type=="well") {
    return(paste0("w", toupper(substr(sha1(x), 1, 3))))
  } else if (type=="fp") {
    return(paste0("fp", toupper(substr(sha1(x), 1, 2))))
  }
}

5.2 Data Handling

Data is extracted and cleaned using Python in simulation.ipynb. The Python notebook is also used to generate a rudimentary config file, but some things (network connectivity) are specified manually.

R is used to:

• Read raw data and config from Excel/CSV files
• Do additional pre-processing that depends on the data available
• Censor sensitive facility names
• Create a graph structure
• Make the data into a JAGS-readable format

5.2.1 Load Data

Reads data from several spreadsheets, including PI data. PI data is special because it has not been pre-processed. It requires additional filtering and basic pre-processing.

# read in config data
configsheets = excel_sheets(configpath)
for (sheet in configsheets) {
  assign(sheet, read_excel(configpath, sheet))
}
stopifnot(!anyDuplicated(well_fp_map$well)) # each well cannot map to multiple flash plants

# read in PI data
PI <- read_excel(pipath, "From PI sheet", skip=1) %>%
  rename(facility = Unit,
         variable = X__1,
         id = X__2,
         description = X__3,
         code = X__4) %>%
  gather(key="datechar", value="value", -c(facility, variable, id, description, code)) %>%
  mutate(date = as.Date(as.numeric(datechar), origin = "1899-12-30"),
         value = as.numeric(value)) %>% select(-c(datechar, id)) %>%
  mutate_if(is.character, tolower) %>%
  mutate(value = as.numeric(value)) %>%
  drop_na(value) %>%
  filter(date >= as.Date("2017-11-01"), date < as.Date(prediction_date)) %>%
  filter(!str_detect(variable, "condition|calc")) %>%
  filter(str_detect(facility, "wk")) 
extra_liq <- PI %>%
  select(facility, date, variable, value) %>% 
  # filter(value>1e-4) %>%
  filter(str_detect(variable, "plot|phase|whp|flow")) %>%
  spread(key=variable, value=value) %>%
  mutate(mf = pmax(`2phase flow`, `fp14  plot flow`, `fp15  plot flow`, `flow`, na.rm=T),
         whp = pmax(`fp14  plot whp`, `fp15  plot whp`, `fp16  plot whp`, `whp`, na.rm=T),
         source = "PI Database") %>%
  select(well=facility, date, whp, mf, source) %>%
  drop_na()

# read in regression data (plus extra)
regression_df = read_excel(regdatapath) %>% mutate(source="Well Tests")
dry_df = PI %>%
  filter(str_detect(facility, "wk")) %>%
  select(facility, date, variable, value) %>%
  # filter(value>1e-2) %>%
  group_by(facility, date) %>%
  spread(key=variable, value=value) %>%
  select(facility, date, `ip sf`, `actual massflow`) %>%
  gather(key="key", value="mf", `ip sf`, `actual massflow`) %>%
  ungroup() %>%
  drop_na() %>%
  rename(well=facility)

5.2.2 Censor names

Censor well and flash plant names using a hash algorithm. Change the flag in setup to disable.

dry_df$well = censor(dry_df$well, "well")
extra_liq$well = censor(extra_liq$well, "well")
fp_constants$fp = censor(fp_constants$fp, "fp")
fp_gen_map$fp = censor(fp_gen_map$fp, "fp")
operating_conditions$well = censor(operating_conditions$well, "well")
regression_df$well = censor(regression_df$well, "well")
well_fp_map$well = censor(well_fp_map$well, "well")
well_fp_map$fp = censor(well_fp_map$fp, "fp")

production_curve_wells = censor(production_curve_wells, "well")
special_wells = censor(special_wells, "well")
tsplotwells = censor(tsplotwells, "well")

5.2.3 Preprocessing

Generate metadata, such as which wells have which data sources, and translate facility names into unique integer IDs. Also creates dummy facilities for multiple purposes.

# combine with extra
regression_df = plyr::rbind.fill(regression_df, extra_liq)

regression_df = regression_df %>%
  mutate(date_numeric = as.numeric(date - base_datetime)) %>%
  mutate(date_numeric=ifelse(date_numeric>0, date_numeric, NA))  # remove dates before baseline
dry_df = dry_df %>%
  filter(well %ni% unique(regression_df$well)) %>%
  mutate(date_numeric = as.numeric(as.POSIXct(date) - base_datetime)) %>%
  mutate(date_numeric=ifelse(date_numeric>0, date_numeric, NA))  # remove dates before baseline
well_fp_map = well_fp_map %>% select(well, fp) %>% drop_na()

# today_numeric = (Sys.time() - base_datetime) %>% as.numeric()
today_numeric = (today_datetime - base_datetime) %>% as.numeric()

# assign unique facility IDs
liq_wells = unique(regression_df$well) # aka production curve wells
dry_wells = unique(dry_df$well)        # aka time series wells
map_wells = unique(well_fp_map$well)   # any well mapped in config

well_names = unique(c(liq_wells, dry_wells))
fp_names = c(well_fp_map$fp, fp_gen_map$fp, fp_constants$fp) %>% unique()

fluid_types = c('ip', 'lp', 'w')
gen_names = gen_constants$gen %>% unique() %>% sort()
ip_gen_names = paste(gen_names, 'ip', sep='_')
lp_gen_names = paste(gen_names, 'lp', sep='_')
w_gen_names = paste(gen_names, 'w', sep='_')
dummy_gen_names = c(ip_gen_names, lp_gen_names, w_gen_names) %>% sort()
all_names = c('DUMMY', well_names, fp_names, dummy_gen_names, gen_names)
ids = 1:length(all_names)
names(ids) = all_names

# check data quality
no_data_wells = map_wells[!map_wells %in% c(liq_wells, dry_wells)]  # see which ones we're completely guessing for
no_map_wells = c(liq_wells, dry_wells)[!c(liq_wells, dry_wells) %in% map_wells]
missing = data.frame(Wells = c(paste(no_map_wells, collapse=", ")),
                     row.names = c("Data available but no FP"))
# print(xtable(missing, type = "latex",
#              caption=paste0("Potential data quality issues. ", names(ids)[71], " is known to be not connected, and ", names(ids)[31], " has an A/B pairing with ", names(ids)[32], "."),
#              label="tab:quality"),
#       file = "../_media/quality.tex")

# add names in data with IDs
regression_df = regression_df %>% mutate(well_id=ids[well])
dry_df = dry_df %>% mutate(well_id=ids[well])
operating_conditions = operating_conditions %>% mutate(well_id=ids[well]) %>% rename(whp_pred=whp)
fp_constants = fp_constants %>% mutate(fp_id=ids[fp])
gen_constants = gen_constants %>% mutate(gen_id=ids[gen]) %>% select(-gen)
well_fp_map = well_fp_map %>% mutate(well_id=ids[well], fp_id=ids[fp]) %>% select(-c(well, fp))
fp_gen_map = fp_gen_map %>% mutate(fp_id=ids[fp], gen_ip_id=ids[gen_ip], gen_lp_id=ids[gen_lp], gen_w_id=ids[gen_w]) %>% select(-c(fp, gen_ip, gen_lp, gen_w))

incomplete.fps = unique(well_fp_map %>%
  filter(is.na(well_id)) %>%
  mutate(fp = names(ids)[fp_id]) %>%
  pull(fp))

5.2.4 Graph

Work out which of the (now uniquely integer-identified) facilities flows to which. Then generates a graphic to check for correctness.

# create connectivity matrix. i flows to j
# wells to FPs
v = matrix(0, nrow=length(ids), ncol=length(ids))
v[1,-1] = 1
for (i in 1:nrow(well_fp_map)) {
  id_i = well_fp_map[[i, 1]]
  id_j = well_fp_map[[i, 2]]
  v[id_i, id_j] = 1
}
# send ip/lp/w flows to dummy gens
for (i in 1:nrow(fp_gen_map)) {
  id_i = fp_gen_map[[i, 1]]
  for (j in 2:ncol(fp_gen_map)) {
    facility_j = names(ids)[fp_gen_map[[i, j]]]
    facility_dummy_j = paste(facility_j, fluid_types[j-1], sep='_')
    id_j = ids[facility_dummy_j]
    if (!is.na(id_j)) {
      v[id_i, id_j] = 1
    }
  }
}
# dummy gens to gens
for (i in 1:nrow(gen_constants)) {
  id_j = gen_constants$gen_id[i]
  facility_j = names(ids)[id_j]
  for (fluid in fluid_types) {
    facility_dummy_i = paste(facility_j, fluid, sep='_')
    id_i = ids[facility_dummy_i]
    v[id_i, id_j] = 1
  }
}

# convert form
m = matrix(0, nrow=nrow(v), ncol=max(colSums(v)))
rownames(m) = all_names
for (i in 1:nrow(v)) {
  for (j in 1:ncol(v)) {
    if (v[[i, j]]==1) {
      m[j, sum(m[j,]>0)+1] = i
    }
  }
}
flows_to = function(well) {
  return(names(ids)[m[well,]][-1])
}

# generate coordinates
dummy_locs = data.frame(name='DUMMY', x=-0.1, y=0)
well_locs = data.frame(name=well_names, x=0, y=seq(1, 1/(length(well_names)-1), length.out=length(well_names)))
fp_locs = data.frame(name=fp_names, x=1, y=seq(0, 1, length.out=length(fp_names)))
gen_dummy_locs = data.frame(name=dummy_gen_names, x=2, y=seq(0, 1, length.out=length(dummy_gen_names)))
gen_locs = data.frame(name=gen_names, x=2.5, y=seq(1/11, 10/11, length.out=length(gen_names)))
locs = rbind(dummy_locs, well_locs, fp_locs, gen_dummy_locs, gen_locs)
locs$id = ids[locs$name]
locs = locs %>% arrange(id)

g = graph_from_adjacency_matrix(v) %>%
  set_vertex_attr('label', value=all_names) %>%
  set_vertex_attr('x', value=as.vector(locs$x)) %>%
  set_vertex_attr('y', value=as.vector(locs$y)) %>%
  set_vertex_attr('label.degree', value=pi) %>%
  as.undirected()
V(g)$size = ifelse(V(g)$label %in% well_names, 4, 8)
V(g)$color = ifelse(V(g)$label %in% dry_wells, "red", ifelse(V(g)$label %in% no_data_wells, "grey", "orange"))
E(g)$color = "black"
E(g)[which(tail_of(g, E(g))$label=="DUMMY")]$color = "grey"

# png("../media/full_network_uncensored.png")
# # par(mar=c(0,3,0,0), family="Times")
# par(mar=c(0,3,0,0))
# plot(g, vertex.label.dist=3,
#      mark.groups = list(wells=ids[well_names], fps=ids[fp_names], gens=ids[gen_names]),
#      mark.col = "#DDDDDD",
#      mark.border = NA)
# text(c(-1, -0.3, 0.4, 0.9), 1.15, c("Wells", "Flash plants", "Dummy gens", "Generators"), cex=1.25)
# dev.off()
plot(g, vertex.label.dist=3,
     mark.groups = list(wells=ids[well_names], fps=ids[fp_names], gens=ids[gen_names]),
     mark.col = "#DDDDDD",
     mark.border = NA)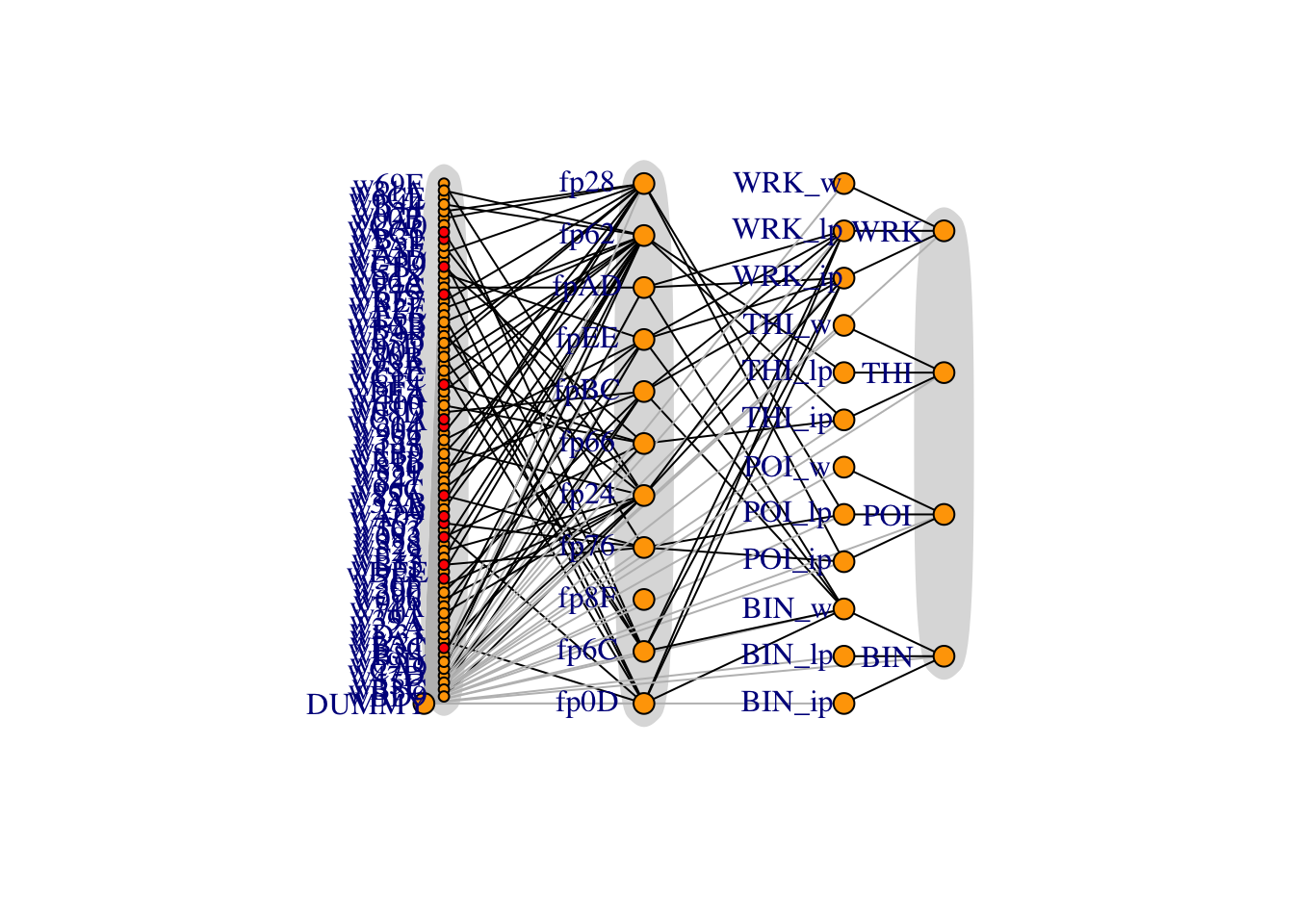

Figure 5.1: Full network diagram, with flows from left to right. Red wells indicate forecasts have been filled in from the PI data without a production curve, and dummy arcs are in grey. Dummy arcs allow IP/LP/water to be split up.

The dummy node is necessary because when indexing a subset of flows that go into a node, this subset cannot be empty. The dummy node has zero mass flowing out of it.

5.2.5 Format Data

JAGS requires data to be real numbers, vectors or matrices in a named list. It can also impute NA values from a distribution. Data wrangling is a significant part of the work - potentially more than the actual model coding and the results analysis combined.

This code also centers some of the covariates so it does not have to be done in JAGS.

\[\begin{equation} x_\text{whp} \leftarrow x_\text{whp} - \overline{x_\text{whp}} \end{equation}\]

regression_list = regression_df %>% select(well_id, whp, mf, date_numeric) %>% as.list()
dry_list = dry_df %>%
  filter(date < prediction_date) %>%
  rename(well_id_dry=well_id, mf_dry=mf, date_numeric_dry=date_numeric) %>% # use these in a different regression
  select(well_id_dry, mf_dry, date_numeric_dry) %>% as.list()
operating_conditions_list = operating_conditions %>% arrange(well_id) %>% select(whp_pred) %>% as.list()
fp_constants_list = as.list(fp_constants)
gen_constants_list = as.list(gen_constants %>% select(gen_id, factor))
facilities = data.frame(id=ids) %>%
  left_join(operating_conditions %>% rename(id=well_id) %>% filter(id %in% ids) %>% select(-well), by='id') %>%
  left_join(gen_constants %>% select(factor, id=gen_id), by='id') %>%
  left_join(fp_constants %>% rename(id=fp_id), by='id') %>%
  filter(id %in% ids) %>%  # in case extras specified in data
  mutate(mf_pred=NA) %>%
  mutate(n_inflows=colSums(v))

well_ids = ids[well_names]
liq_well_ids = ids[liq_wells]
dry_well_ids = ids[dry_wells]
fp_ids = ids[fp_names]
ip_gen_ids = ids[ip_gen_names]
lp_gen_ids = ids[lp_gen_names]
w_gen_ids = ids[w_gen_names]
gen_ids = ids[gen_names]

# force all mass to IP steam
dry_fps = c("poi dry", "direct ip")
dry_fp_ids = ids[dry_fps]
facilities$hf_ip[facilities$id %in% dry_fp_ids] = 10
facilities$hfg_ip[facilities$id %in% dry_fp_ids] = 10
facilities_list = facilities %>% select(-id) %>% as.list()

# experimental TS data matrix for dry wells
ar_order = 1
empty = setNames(data.frame(matrix(ncol = length(all_names), nrow = 0)), all_names)
drymatrix = dry_df %>% 
  select(well, date_numeric, mf) %>% 
  spread(well, mf) %>% 
  select(-date_numeric)
drymatrix = empty %>%
  full_join(drymatrix) %>%
  as.matrix()
ar_well_ids = which(complete.cases(t(drymatrix[1:(ar_order+1),])))
ar_wells = names(ids)[ar_well_ids]
# which wells can we not use AR for
dry_no_ar_wells = dry_wells[!dry_well_ids %in% ar_well_ids]
dry_no_ar_well_ids = ids[dry_no_ar_wells]

# insert production curve predictions
stopifnot(all(tsplotwells %in% dry_df$well))
tsplotwells = ar_wells
days_since_last = as.integer(today_datetime - as.POSIXct(max(dry_df$date)))
prod = expand.grid(whp_prod=seq(6, 16, length.out=10),
                  well_id_prod=ids[production_curve_wells])
ts = expand.grid(date_numeric_ts=seq(min(dry_df$date_numeric), max(dry_df$date_numeric)+days_since_last, length.out=10),
                 well_id_ts=ids[tsplotwells])
prod_list = prod %>% as.list
ts_list = ts %>% as.list

# extend matrix for prediction
drymatrix = rbind(drymatrix, matrix(NA, nrow=days_since_last, ncol=ncol(drymatrix)))

# combine into one list
data = c(regression_list, dry_list, facilities_list, prod_list, ts_list,
         list(well_ids=well_ids, liq_well_ids=liq_well_ids, 
              dry_well_ids=dry_well_ids, dry_no_ar_well_ids=dry_no_ar_well_ids,
              fp_ids=fp_ids,
              gen_ids=gen_ids, ip_gen_ids=ip_gen_ids, lp_gen_ids=lp_gen_ids, w_gen_ids=w_gen_ids,
              today_numeric=today_numeric, m=m, dummy=1,
              ts=drymatrix, ts_ar=drymatrix, ts_ema=drymatrix, ar_well_ids=ar_well_ids))
# data$whp_pred[is.na(data$whp_pred)] <- mean(data$whp_pred, na.rm=T)

# center covariates
mean_whp <- mean(data$whp, na.rm=T)
mean_date_numeric <- mean(data$date_numeric, na.rm=T)

data$whp_c <- data$whp - mean_whp
data$whp_pred_c <- data$whp_pred - mean_whp
data$whp_prod_c <- data$whp_prod - mean_whp
data$date_numeric_c <- data$date_numeric - mean_date_numeric
data$today_numeric_c <- data$today_numeric - mean_date_numeric
data$date_numeric_dry_c <- data$date_numeric_dry - mean_date_numeric
data$date_numeric_ts <- data$date_numeric_ts - mean_date_numeric

pidataplot = ggplot(regression_df %>% filter(source=="PI Database"), aes(x=whp, y=mf, color=well)) +
  geom_point() +
  labs(title=paste("PI Regression Data from", min(extra_liq$date), "to", max(extra_liq$date)),
       x="Well-head pressure (bar)", 
       y="Mixed-phase mass flow (T/h)",
       color="Well") +
  guides(color=guide_legend(ncol=2))# +
  # ggsave('../_media/pi_data.png', width=24.7, height=12, units='cm')
ggplotly(pidataplot)

Figure 5.2: One month of the most recent regression data from the PI database. We use a combination of well test data (not shown) to estimate the regression parameters, and this PI data to increase the weight and precision for short-term forecasts. Note how PI data is tightly clustered – this forces regressions to fit closely and is desirable if our predicted regressors are close to the PI data.

5.3 Model

JAGS accepts a model in a text string. It uses an R-like syntax, but is a declarative language not sequential. We do basic manipulation of the output traces.

code = "
data {
  D <- dim(ts)
}
model {
  ##############################################
  # fit individual regressions to liquid wells #
  ##############################################
  for (i in 1:length(mf)) {
    mu[i] <- Intercept[well_id[i]] + beta_whp[well_id[i]] * whp_c[i] + beta_date[well_id[i]] * date_numeric_c[i]
    mf[i] ~ dnorm(mu[i], tau[well_id[i]])
    mf_fit[i] ~ dnorm(mu[i], tau[well_id[i]])
    # mf_fit[i] ~ dnorm(mu[i]*measurement_error_factor[i], tau[well_id[i]])
    # measurement_error_factor[i] ~ dunif(0.9, 1.1)
  }
  # fit regression to dry wells
  for (i in 1:length(mf_dry)) {
    mu_dry[i] <- Intercept[well_id_dry[i]] + beta_date[well_id_dry[i]] * date_numeric_dry_c[i]
    mf_dry[i] ~ dnorm(mu_dry[i], tau[well_id_dry[i]])
    mf_dry_fit[i] ~ dnorm(mu_dry[i], tau[well_id_dry[i]])
    # measurement_error_factor_dry[i] ~ dunif(0.9, 1.1)
  }
  for (j in dry_well_ids) {
    Intercept[j] ~ dnorm(0, 1e-12)
    beta_date[j] ~ dnorm(0, 1e-12)
    tau[j] ~ dgamma(1e-12, 1e-12)
  }
  # experimental AR1 model for dry wells
  for (j in ar_well_ids) {
    for (t in 2:D[1]) {
      mu_ar[t,j] <- c_ar[j] + theta_ar[j]*ts_ar[t-1,j]
      ts_ar[t,j] ~ dnorm(mu_ar[t,j], tau_ar[j]) T(0,)
    }
    theta_ar[j] ~ dnorm(0, 1e-12)
    c_ar[j] ~ dnorm(0, 1e-12)
    tau_ar[j] ~ dgamma(1e-12, 1e-12)
  }
  # experimental EWMA model (use at your own risk)
  for (j in ar_well_ids) {
    for (t in 2:D[1]) {
      mu_ema[t,j] <- alpha*mu_ema[t-1,j] + (1-alpha)*ts_ema[t,j]
      ts_ema[t,j] ~ dnorm(mu_ema[t-1,j], tau_ema[j]) T(0,)
    }
    mu_ema[1,j] <- ts_ema[1,j]
    theta_ema[j] ~ dnorm(0, 1e-12)
    c_ema[j] ~ dnorm(0, 1e-12)
    tau_ema[j] ~ dgamma(1e-12, 1e-12)
  }
  alpha ~ dbeta(0.5, 0.5)

  # HIERARCHICAL
  # fills in for any missing wells
  for (j in liq_well_ids) {
    Intercept[j] ~ dnorm(mu_Intercept, tau_Intercept)
    beta_whp[j] ~ dnorm(mu_beta_whp, tau_beta_whp)
    # beta_whp2[j] ~ dnorm(mu_beta_whp2, tau_beta_whp2)
    beta_date[j] ~ dnorm(mu_beta_date, tau_beta_date)
    tau[j] ~ dgamma(1e-12, 1e-12)
    sd[j] <- 1/max(sqrt(tau[j]), 1e-12)
  }

  # fill in any missing data
  for (i in 1:length(mf)) {
    date_numeric_c[i] ~ dnorm(mu_date_numeric, tau_date_numeric)
  }
  mu_date_numeric ~ dnorm(0, 1e-12)
  tau_date_numeric ~ dnorm(1e-12, 1e-12)
  
  # set hyperparameters
  mu_Intercept ~ dnorm(0, 1e-12)
  mu_beta_whp ~ dnorm(0, 1e-12)
  # mu_beta_whp2 ~ dnorm(0, 1e-12)
  mu_beta_date ~ dnorm(0, 1e-12)
  tau_Intercept ~ dgamma(1e-12, 1e-12)
  tau_beta_whp ~ dgamma(1e-12, 1e-12)
  # tau_beta_whp2 ~ dgamma(1e-12, 1e-12)
  tau_beta_date ~ dgamma(1e-12, 1e-12)

  #####################################
  # production curve for verification #
  #####################################
  for (i in 1:length(whp_prod)) {
    mu_prod[i] <- Intercept[well_id_prod[i]] + beta_whp[well_id_prod[i]] * whp_prod_c[i] + beta_date[well_id_prod[i]] * today_numeric_c
    # mf_prod[i] ~ dnorm(mu_prod[i], tau[well_id_prod[i]])
    mf_prod[i] <- mu_prod[i]
  }
  for (i in 1:length(date_numeric_ts)) {
    mu_ts[i] <- Intercept[well_id_ts[i]] + beta_date[well_id_ts[i]] * date_numeric_ts[i]
    mf_ts[i] ~ dnorm(mu_ts[i], tau[well_id_ts[i]])
  }

  #########################################################
  # simple model to fill in missing FP enthalpy constants #
  #########################################################
  for (i in fp_ids) {
    # missing fp constants
    hf_ip[i] ~ dgamma(param[1], param[7])
    hg_ip[i] ~ dgamma(param[2], param[8])
    hfg_ip[i] ~ dgamma(param[3], param[9])
    hf_lp[i] ~ dgamma(param[4], param[10])
    hg_lp[i] ~ dgamma(param[5], param[11])
    hfg_lp[i] ~ dgamma(param[6], param[12])
  }
  for (i in c(1, well_ids)) { 
    h[i] ~ dgamma(param[13], param[14])
    whp_pred_c[i] ~ dnorm(param[15], param[16])
  } # missing well constants
  for (i in 1:16) { param[i] ~ dgamma(1e-12, 1e-12) }               # uniform priors

  ########################################
  # make predictions (the stuff we want) #
  ########################################
  mf_pred[dummy] <- 0  # dummy well
  ip_sf[dummy] <- 0
  lp_sf[dummy] <- 0
  wf[dummy] <- 0
  
  # use production curve
  for (j in liq_well_ids) {
    mf_pred[j] <- max(Intercept[j] + beta_whp[j] * whp_pred_c[j] + beta_date[j] * today_numeric_c, 0)
  }
  # use naive TS reg
  for (j in dry_well_ids) { #dry_no_ar_well_ids) {
    mf_pred[j] <- max(Intercept[j] + beta_date[j] * today_numeric_c, 0)
  }
  # use AR(1)
  # for (j in ar_well_ids) {
  #   mf_pred[j] <- mu_ar[D[1], j]
  # }

  for (i in fp_ids) {
    mf_pred[i] <- sum(mf_pred[m[i,1:n_inflows[i]]])
    h[i] <- sum(mf_pred[m[i, 1:n_inflows[i]]] * h[m[i, 1:n_inflows[i]]]) / ifelse(mf_pred[i]!=0, mf_pred[i], 1)

    ip_sf[i] <- min(max((h[i] - hf_ip[i]), 0) / hfg_ip[i], 1) * mf_pred[i]
    lp_sf[i] <- min(max((min(hf_ip[i], h[i]) - hf_lp[i]), 0) / hfg_lp[i], 1) * (mf_pred[i] - ip_sf[i])

    total_sf[i] <- ip_sf[i] + lp_sf[i]
    wf[i] <- mf_pred[i] - total_sf[i]
  }
  # dummy gens and actual gens
  for (i in ip_gen_ids) { mf_pred[i] <- sum(ip_sf[m[i, 1:n_inflows[i]]]) }
  for (i in lp_gen_ids) { mf_pred[i] <- sum(lp_sf[m[i, 1:n_inflows[i]]]) }
  for (i in w_gen_ids) { mf_pred[i] <- sum(wf[m[i, 1:n_inflows[i]]]) }
  for (i in gen_ids) {
    mf_pred[i] <- sum(mf_pred[m[i,1:n_inflows[i]]])
    power[i] <- mf_pred[i] / mu_factor[i]
    mu_factor[i] ~ dunif(0.95*factor[i], 1.05*factor[i])  # uncertainty from email
  }
  total_power <- sum(power[gen_ids])
}
"
# cat(code, file="model.txt")

vars =  c('mf_fit',
          'mf_dry_fit',
          'mf_ts',
          'mf_prod',
          'mf_pred',
          'beta_date',
          'sd',
          'power',
          'total_sf',
          'mu_ar',
          'ts_ar',
          'mu_ema',
          'ts_ema',
          'alpha',
          'ip_sf',
          'lp_sf',
          'wf',
          paste0('h[', fp_ids, ']'),
          paste0('mu_', c('Intercept', 'beta_whp', 'beta_date')),
          'total_power')
n_chains = 2
burn_in = 100

model = jags.model(textConnection(code), data, n.chains=n_chains)

## Compiling data graph
##    Resolving undeclared variables
##    Allocating nodes
##    Initializing
##    Reading data back into data table
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 6257
##    Unobserved stochastic nodes: 3918
##    Total graph size: 29435
## 
## Initializing model

update(model, burn_in)
out = coda.samples(model, n.iter=round(n_steps/n_chains), variable.names=vars)
outmatrix = as.matrix(out)
outframe = as.data.frame(outmatrix) %>%
  gather(key=facility, value=value) %>%
  mutate(variable=gsub("\\[.*$", "", facility), facility=parse_number(facility, na=c("NA")))
outframe$facility = factor(names(ids)[outframe$facility])
outframe %>% tail %>% kable(caption="A few samples.") %>% kable_styling

Table 5.1: A few samples.

	facility	value	variable
5653995	fp8F	0	wf
5653996	fp8F	0	wf
5653997	fp8F	0	wf
5653998	fp8F	0	wf
5653999	fp8F	0	wf
5654000	fp8F	0	wf

5.4 Convergence Tests

One of the difficulties with MCMC approximations is they often require a burn-in (warm-up) period before settling into the stationary distribution of the Markov chain. Only the stationary distribution corresponds to the joint distribution we wish to sample from. In most practical uses, there is no way to predict convergence, so we diagnose convergence by monitoring the sample trace and running diagnostic tests.

5.4.1 Trace plots

Poor convergence or mixing is indicated by a strong trend at the beginning of the trace plot.

trace1 <- outframe %>%
  filter(variable=='mf_pred', facility==censor('wk256', "well")) %>%
  mutate(index = 1:nrow(.))
trace2 <- outframe %>%
  filter(variable=='total_power') %>%
  mutate(index = 1:nrow(.))
trace3 <- outframe %>%
  filter(variable=='mu_Intercept') %>%
  mutate(index = 1:nrow(.))
traceplot = ggplot(trace1, aes(x=index, y=value, color=variable)) +
  geom_line(alpha=0.75) +
  geom_line(data=trace2, alpha=0.75) +
  geom_line(data=trace3, alpha=0.75) +
  coord_cartesian(xlim = c(max(trace1$index)-1000, max(trace1$index))) +
  labs(title="Trace Plot (Single chain)", x="Iteration", y="Parameter value", color="Variable")# +
  # ggsave('../media/trace_plot.png', width=16, height=8, units='cm')
# ggplotly(traceplot)
traceplot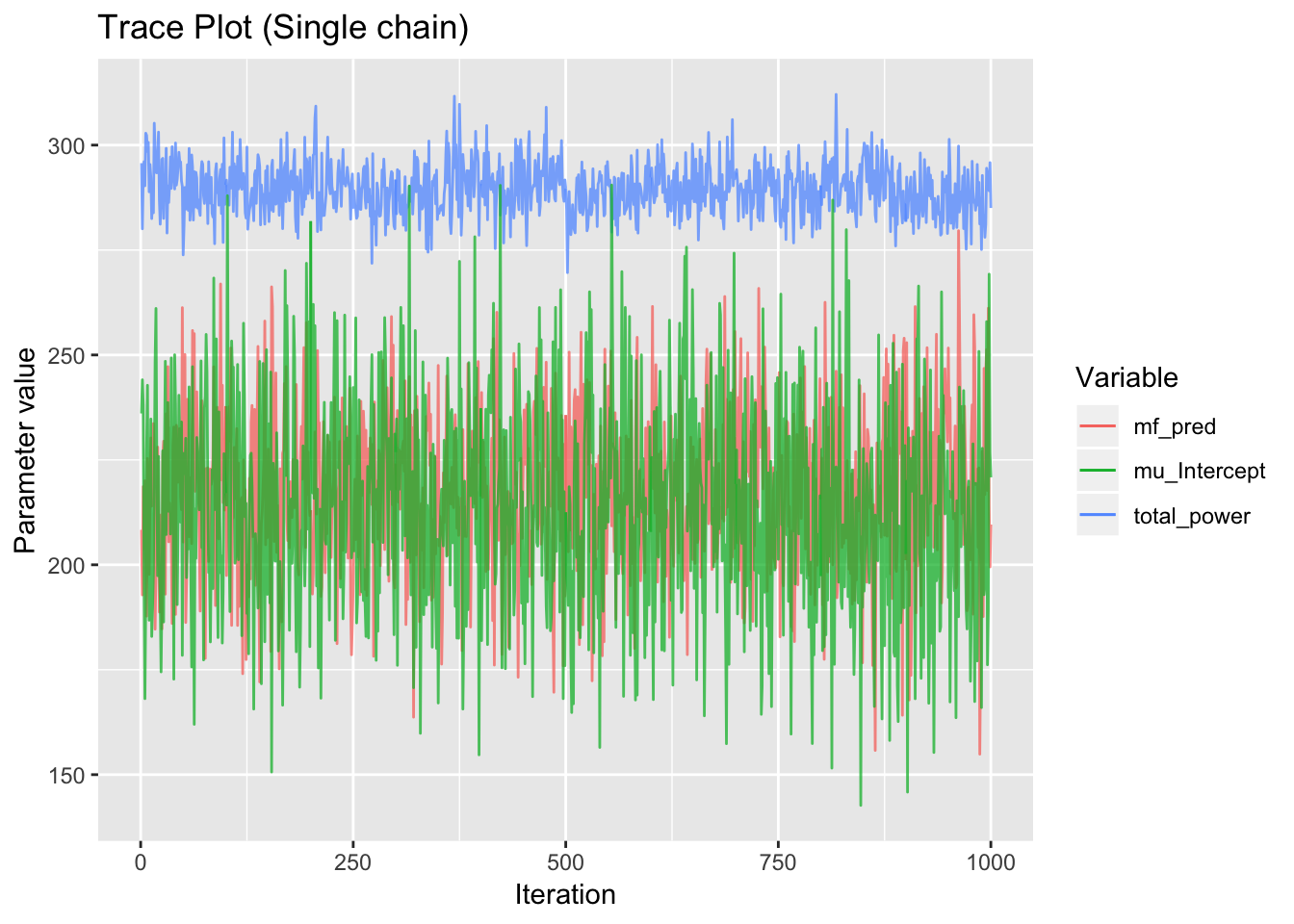

Figure 5.3: Example trace plots displaying normal behaviour. The sampler appears to have reached its equilibrium distribution with no trend.

5.4.2 Geweke

Geweke’s convergence diagnostic for MCMC samples tests for equality of the means in the first 10% and last 50% of the trace. The means will be equal if the sample is drawn from a stationary distribution, indicating the burn-in period has been successfully excluded.

If true univariate convergence has been achieved, we expect 95% of variables to pass Geweke’s test with a z-score less than 1.96 with 95% confidence.

# 100 random var because it takes too long
random_var_ix = sample.int(ncol(outmatrix), 100)
geweke.out = geweke.diag(out[,random_var_ix])
geweke.df = data.frame(Index = 1:length(unlist(geweke.out)),
                       z = unlist(geweke.out[1])) %>%
  mutate(out = ifelse(abs(z)>1.96, T, F)) %>%
  drop_na()

proportion_out = sum(geweke.df$out) / nrow(geweke.df)
gewekeplot = ggplot(geweke.df, aes(x=Index, y=z)) +
  geom_point() +
  geom_hline(data=data.frame(value=c(1.96,-1.96)), aes(yintercept=value), color='red') +
  labs(title=paste0("Geweke z-score. ", round(proportion_out, 2)*100,
                    "% of points lie outside the 95% confidence interval."))# +
  # ggsave('../_media/geweke.png', width=24.7, height=6, units='cm')
ggplotly(gewekeplot)

Figure 5.4: More than 5% of z-scores outside the confidence interval, indicating the chains have not converged and are either too short or contain burn-in.

5.4.3 Gelman

The Gelman-Rubin convergence diagnostic gives the potential scale reduction factor (PSRF) for each parameter. This requires at least two independent chains and tests whether the chains have converged to identical distributions. If the chains have not converged, the scale reduction factors will have upper confidence limits greater than one. It is possible that when run indefinitely, the variance of the parameter estimate could shrink by the PSRF.

gelman.out = gelman.diag(out[,c(paste0('mf_pred[', 8:9, ']'),
                                'beta_date[9]', 'mu_beta_whp', 'mu_beta_date',
                                'mu_Intercept', 'total_power')])[[1]] %>% 
  as.data.frame()
gelman.out %>% kable(caption="Gelman-Rubin test statistics") %>% kable_styling

Table 5.2: Gelman-Rubin test statistics

	Point est.	Upper C.I.
mf_pred[8]	1.0017218	1.009482
mf_pred[9]	1.0001877	1.003918
beta_date[9]	1.0277830	1.114368
mu_beta_whp	0.9999491	1.002421
mu_beta_date	1.0084465	1.016942
mu_Intercept	0.9999066	1.003478
total_power	1.0004981	1.000559

Some of the upper CIs are slightly greater than one, but not significantly. Large PSRFs are acceptable if they are in components of the network that do not affect parameters of interest.

5.4.4 Raftery

Raftery’s diagnostic gives the number of samples required to estimate a quantile (or credible interval) to a certain accuracy. In this notebook we only run 1000 samples so it says we do not have enough.

raftery.out = raftery.diag(out[,c(paste0('mf_pred[', 8:9, ']'),
                                  'beta_date[9]', 'mu_beta_whp', 'mu_beta_date',
                                  'mu_Intercept', 'total_power')])
raftery.out[[1]]

## 
## Quantile (q) = 0.025
## Accuracy (r) = +/- 0.005
## Probability (s) = 0.95 
## 
## You need a sample size of at least 3746 with these values of q, r and s

5.5 Posteriors

We generate density plots in their most basic forms without post-processing.

5.5.1 Well Mass Flow

g1 = ggplot(outframe %>% 
              filter(facility %in% well_names, variable=="mf_pred", value>0) %>%
              mutate(source = ifelse(facility %in% dry_wells, "PI time series", "Production curve")), 
            aes(x=value, fill=facility)) +
  geom_density(aes(y=..scaled..), alpha=0.5, color=NA) + xlim(0, NA) +
  facet_grid(source~.) +
  theme(axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  guides(fill=F) +
  labs(title=paste("Posterior Well Mass Flows for", prediction_date), 
       x="Mass flow (T/h)", y="Scaled density", fill="Facility")# +
  # ggsave('../media/mf_wells_sans.png', width=12, height=8, units='cm')
ggplotly(g1, tooltip=c('facility', 'value'))

Figure 5.5: Posterior mass flows for all 71 wells, divided into wells with production curves and wells with a simple time-series. Wells show large variations in mean mass flow and variance.

5.5.2 Decline Rate

An operator might like to see which wells are declining the fastest.

g2 = ggplot(outframe %>% filter(variable=="beta_date", facility %in% special_wells),
            aes(x=value, fill=facility)) +
  geom_density(alpha=0.5, color=NA) +
  geom_vline(xintercept = 0, color="red") +
  labs(title="Posterior Decline Rate of Test Data", 
       x="beta_date (T/h/d)", y="Density", fill="Facility") +
  theme(axis.text.y=element_blank(),
        axis.ticks.y=element_blank())# +
  # guides(fill=F) +
  # ggsave('../media/beta_date_sans.png', width=12, height=8, units='cm')
ggplotly(g2, tooltip=c('facility', 'value'))

Figure 5.6: Decline rates for \(\beta_\text{date}\).

5.5.3 Gen Mass Flow

g4 = ggplot(outframe %>% filter(facility %in% gen_names, variable=="mf_pred", value>0),
            aes(x=value, fill=facility)) +
  geom_density(aes(y=..scaled..), alpha=0.5, color=NA) + xlim(0, NA) + 
  theme(axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  labs(title=paste("Posterior Generator Values for", prediction_date), 
       x="Mass flow (T/h)", y="Scaled density", fill="Facility")# +
  # ggsave('../_media/mf_gens.png', width=24.7, height=10, units='cm')
ggplotly(g4, tooltip=c('facility', 'value'))

Figure 5.7: Generator mass flow estimates.

5.5.4 Gen Power

g5.actual = data.frame(facility = c("WRK", "THI", "POI", "BIN"),
                       value = c(121.73567, 172.18096, 51.53028, 9.98687))
g5 = ggplot(outframe %>% filter(facility %in% gen_names, variable=="power", value>0),
            aes(x=value, fill=facility)) +
  geom_density(aes(y=..scaled..), alpha=0.5, color=NA) + xlim(0, NA) +
  # geom_vline(data=g5.actual, aes(xintercept=value, color=facility)) +
  theme(axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  labs(x="Power (MW)", y="Scaled density", fill="Facility")# +
  # ggsave('../_media/power_gens.png', width=24.7, height=10, units='cm')

ggplotly(g5, tooltip=c('facility', 'value'))

Figure 5.8: Generator power estimates

tsgrob4.5 = grid_arrange_shared_legend(g4, g5, nrow=2, ncol=1, position = "right")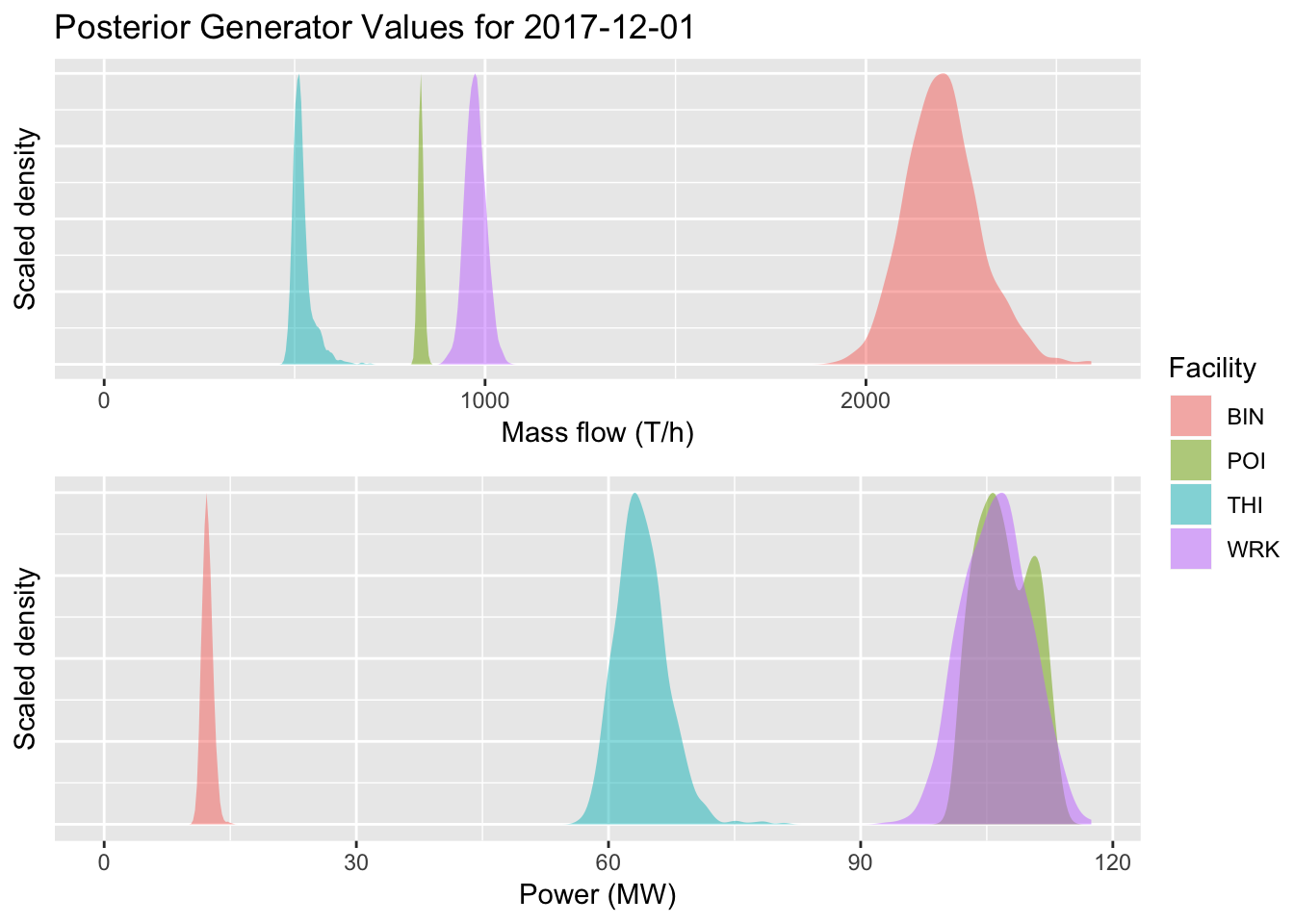

Figure 5.8: Generator power estimates

# ggsave('../media/gens_sans.png', tsgrob4.5, width=12, height=8, units='cm')

5.5.5 Well Standard Deviation

tb6 <- outframe %>% filter(variable=="sd") %>% select(facility, value) %>%
  mutate(well=factor(facility)) %>%
  group_by(well) %>%
  summarise(Mean = mean(value), 
            `Lower 2.5%` = quantile(value, 0.025), 
            `Upper 97.5%` = quantile(value, 0.975)) %>%
  mutate_if(is.numeric, round, 3) %>%
  inner_join(regression_df %>% 
               mutate(well=factor(names(ids)[well_id])) %>% 
               group_by(well) %>% 
               summarise(n=n()), by="well")
g6 = ggplot(outframe %>% filter(variable=="sd") %>% filter(facility %in% special_wells),
            aes(x=value, fill=facility)) +
  geom_density(alpha=0.5, color=NA) + coord_cartesian(xlim=c(0, max(tb6$`Upper 97.5%`))) +
  theme(axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  labs(title="Posterior Flow Deviation Estimates", 
       x="Standard deviation", y="Density", fill="Facility")# +
  # ggsave('../_media/standard_deviation.png', width=24.7, height=10, units='cm')
ggplotly(g6, tooltip=c('facility', 'value'))

Figure 5.9: Estimates for standard deviation in well mass flow.

5.6 Advanced Analysis

5.6.1 High Variance wells

nrow.source = function(df, facilityname, sourcename) {
  return(nrow(df %>% filter(well==facilityname, source==sourcename)))
}
well_summaries = outframe %>%
  filter(facility %in% well_names, variable=="mf_pred") %>%
  group_by(facility) %>%
  summarise(mean = mean(value),
            sd = sd(value),
            n_test = nrow.source(regression_df, unique(facility),"Well Tests"),
            n_pi = nrow.source(regression_df, unique(facility), "PI Database"),
            use.test = ifelse(n_test>0, "Test data", "No test data"),
            use.pi = ifelse(n_pi>0, "PI data", "No PI data")) %>%
  arrange(desc(sd))
well_summaries$production.curve = ifelse(well_summaries$facility %in% liq_wells,
                                         "Production curve", "Time series")

# fp_summaries = list(fp14 = well_summaries %>% filter(facility %in% flows_to(censor('fp14', 'fp'))),
#                     fp15 = well_summaries %>% filter(facility %in% flows_to(censor('fp15', 'fp'))),
#                     fp16 = well_summaries %>% filter(facility %in% flows_to(censor('fp16', 'fp'))))
# for (fp in names(fp_summaries)) {
#   print(xtable(fp_summaries[[fp]] %>% select(-c(use.test, use.pi, production.curve)),
#                type = "latex",
#                caption=paste("Data methods feeding flash plant", censor(fp, 'fp')),
#                label=paste0("tab:well_summaries_", fp)),
#       table.placement = "H",
#       file = paste0("../_media/summaries_", fp, ".tex"))
# }

n_summaries = well_summaries %>%
  group_by(use.pi, use.test) %>%
  count()

sourceplot = ggplot(well_summaries, aes(x=1, y=log(sd))) +
  geom_boxplot(fill='steelblue') +
  # geom_label(data=n_summaries, 
  #            aes(x=-Inf, y=-Inf, hjust=0, vjust=0, 
  #                label=paste0("n=", n), family="Times New Roman"),
  #            label.size=0, fill='white') +
  geom_text(data=n_summaries, 
            aes(x=-Inf, y=-Inf, hjust=0, vjust=0, 
                label=paste0("n=", n), family="Times New Roman")) +
  facet_grid(.~ use.pi + use.test) +
  theme(axis.text.x=element_blank(),
        axis.ticks.x=element_blank()) +
  labs(title="Differences in Production Error by Data Source", 
       x="Production curve data source", y="log(standard deviation)")# +
  # ggsave('../_media/error_source.png', width=24.7*0.5, height=6, units='cm')
ggplotly(sourceplot)

Figure 5.10: Facets of the data sources for the mass flow’s standard deviation. No data (far left) means there was no curve – these mass flows were predicted by time series on PI mass-flow data. \(n\) is the number of wells, and standard deviation is calculated as \(\text{sd}(\hat{\dot{m}}_j)\) for each well. Lower values mean the samples for mass flow were more concentrated, but this is not necessarily a good thing if it means we are under-estimating uncertainty.

sourcetab = well_summaries %>%
  select(facility, mean, sd, n_test, n_pi) %>%
  mutate(error.coef = sd/mean)
# print(xtable(sourcetab %>% head(), type = "latex",
#              caption="Upon inspection of the wells with the most variance, there is no immediate cause for high variance. This requires further investigation.",
#              label="tab:well_summaries"),
#       table.placement = "h",
#       file = "../_media/well_summaries.tex")
# sourcetab %>% datatable(caption = "Production errors and data sources",
#                         options=list(scrollX=T))
sourcetab %>% kable(caption="Production errors and data sources") %>%
  kable_styling %>% scroll_box(height="400px", width="100%")

Table 5.3: Production errors and data sources

facility	mean	sd	n_test	n_pi	error.coef
wC00	63.9981457	99.0531079	2	0	1.5477497
wF8E	91.7251623	79.1308073	4	0	0.8626947
wCA0	92.3188475	50.0940956	26	0	0.5426205
wC98	322.6368801	47.6007790	28	0	0.1475367
w74A	162.2008252	39.0661915	36	0	0.2408508
w06A	74.0340774	26.6859815	10	0	0.3604554
w354	63.9002997	26.3140532	24	0	0.4117986
w416	99.5325350	26.0573663	31	0	0.2617975
wB84	111.3918407	25.1605822	13	0	0.2258746
w518	185.0984037	22.5775834	31	0	0.1219761
wF4C	123.1824162	21.8411400	31	0	0.1773073
wE66	28.6914173	21.4476007	10	0	0.7475267
w69D	154.3584804	20.5179189	26	0	0.1329238
w390	127.8122133	19.6294856	32	0	0.1535807
w55E	94.2931147	19.6032300	26	0	0.2078967
wC1C	218.3968326	18.3982077	32	30	0.0842421
wA2E	87.9092983	18.2419519	27	30	0.2075088
w906	322.9491506	16.4306409	29	30	0.0508769
w3AE	393.2207197	15.8516454	34	30	0.0403123
w096	420.6752761	15.3806557	41	30	0.0365618
w30F	334.8851488	14.7214381	34	30	0.0439597
wE1B	118.6753231	14.5747640	16	0	0.1228121
w93A	377.6639378	14.0461418	41	30	0.0371922
wB8C	132.7815690	13.4422456	26	0	0.1012358
w31A	305.7295697	13.1307510	31	30	0.0429489
w70B	157.5224458	12.0554308	26	0	0.0765315
w328	132.4247509	11.8561516	25	30	0.0895312
w96C	62.6956628	10.7038158	47	0	0.1707266
w880	152.2787464	10.4818345	45	0	0.0688332
w05D	634.5382017	9.8903755	36	30	0.0155867
w6CE	205.9843676	9.8516171	20	0	0.0478270
w39A	196.6249909	9.6842463	37	30	0.0492524
w2A1	202.3288276	9.5404853	92	0	0.0471534
w08D	252.7168867	9.4331129	31	0	0.0373268
w69F	107.0533518	8.7552678	44	0	0.0817842
w47D	375.6029229	8.6025506	52	30	0.0229033
w4AB	7.5881982	7.6685007	0	30	1.0105825
w024	85.6494318	6.8252907	6	30	0.0796887
wB4B	149.2741061	6.7212862	18	0	0.0450265
wDEE	232.9507090	6.3186185	48	30	0.0271243
wE4D	132.7990085	5.8186998	18	0	0.0438158
w503	44.3078482	5.6931302	18	0	0.1284903
wA37	295.9185023	4.9354244	33	30	0.0166783
wBE7	250.1393053	4.8871555	37	30	0.0195377
w00B	269.6026030	4.5148820	32	30	0.0167464
w847	461.7868877	4.3236383	5	30	0.0093628
w3AB	198.6393599	3.5121365	38	30	0.0176810
w521	309.2015985	3.2274131	37	30	0.0104379
w145	221.4903843	3.1958085	34	30	0.0144287
wCA9	207.5767543	2.6306717	7	30	0.0126732
w001	226.6452359	2.3592042	39	30	0.0104092
w167	34.9986266	1.6260144	0	0	0.0464594
wBD9	14.4652592	0.9671309	0	30	0.0668589
w85A	21.8041081	0.8425673	0	0	0.0386426
w529	13.1189572	0.5331816	0	30	0.0406421
wFEA	60.3061260	0.4627170	0	30	0.0076728
wE15	45.5548760	0.4221435	0	30	0.0092667
w5F8	1.3259438	0.3815764	0	0	0.2877772
wB55	6.8469432	0.3056685	0	0	0.0446431
wA09	1.6093490	0.2899152	0	0	0.1801444
wB44	30.8431955	0.2091660	0	30	0.0067816
w8F4	6.6804815	0.1841890	0	0	0.0275712
w8B9	22.6098826	0.1777644	0	30	0.0078622
w23A	23.3865492	0.1576293	0	30	0.0067402
wD33	0.1544295	0.1394357	0	30	0.9029088
w701	14.9971632	0.1082694	0	30	0.0072193
wCB9	26.3655839	0.0857350	0	0	0.0032518
w083	8.1267305	0.0836531	0	0	0.0102936
w22A	58.8893110	0.0676537	0	30	0.0011488
w6C6	0.7690489	0.0396560	0	0	0.0515650
wB3C	9.5086399	0.0318312	0	0	0.0033476
w675	0.0019461	0.0019686	0	0	1.0115735
wB31	0.0012408	0.0012583	0	0	1.0140403
wC1A	0.0006930	0.0004405	0	0	0.6357041
w204	0.0000000	0.0000000	0	0	NaN

5.6.2 Regression Fits

prod = as.data.frame(outmatrix) %>%
  select(contains('prod')) %>%
  gather(key=facility, value=value) %>%
  mutate(which=parse_number(facility)) %>%
  mutate(whp=data$whp_prod[which],
         well = names(ids)[data$well_id_prod[which]]) %>%
  rename(mf=value) %>%
  group_by(well, whp) %>%
  summarise(lower=quantile(mf, 0.025),
            upper=quantile(mf, 0.975),
            mean=mean(mf))

plotdata = regression_df %>%
  filter(well_id %in% ids[production_curve_wells]) %>%
  mutate(datetime = factor(as.Date(date))) %>%
  mutate(source = factor(source, levels=c("Well Tests", "PI Database")))

# regression plot
regplot = ggplot(prod, aes(x=whp)) +
  geom_line(aes(y=mean, color=well)) +
  geom_ribbon(aes(ymin=lower, ymax=upper, fill=well), alpha=0.25) +
  geom_point(data=plotdata, aes(y=mf, color=well, size=date, shape=source), alpha=0.5) +
  labs(title="Linear Regression on Test and PI Data", 
       x="Well-head pressure (bar)", y="Mass flow (T/h)", 
       color="Well", shape="Data source", size="Date", fill="Well") +
  coord_cartesian(xlim=c(min(plotdata$whp)*0.9,max(plotdata$whp)*1.1),
                  ylim=c(0,max(plotdata$mf)*1.1))# +
  # ggsave('../_media/production_curve.png', width=24.7*0.48, height=24.7*0.48, units='cm')
ggplotly(regplot)

Figure 5.11: We expect the curves to make better predictions near the PI data after inclusion. Forecasted production curves for December 1st, and shaded regions are 95% credible intervals.

saveWidget(ggplotly(regplot), "regplot.html")

5.6.3 Time Series Plots

tsplotwells = ar_wells
ts_fit = as.data.frame(outmatrix) %>%
  select(contains('mf_ts')) %>%
  gather() %>%
  mutate(index = parse_number(key)) %>% select(-key) %>%
  group_by(index) %>%
  summarise(lower=quantile(value, 0.025),
            upper=quantile(value, 0.975),
            mean=mean(value)) %>%
  cbind(ts) %>%
  mutate(well = factor(names(ids[well_id_ts])),
         date_numeric = date_numeric_ts)

# actual observations
tsplotdata = dry_df %>%
  filter(well_id %in% ids[tsplotwells]) %>%
  mutate(datetime = factor(as.Date(date)),
         facility = well)

# experimental AR1 time series
ar_fit = as.data.frame(outmatrix) %>%
  select(contains("mu_ar")) %>%
  gather() %>%
  mutate(date_numeric = as.numeric(str_extract(key, "(?<=\\[)(.*?)(?=,)")) + min(dry_df$date_numeric) - 1,
         facility = names(ids)[as.numeric(str_extract(key, "(?<=,)(.*?)(?=\\])"))]) %>%
  select(facility, date_numeric, value) %>%
  group_by(facility, date_numeric) %>%
  summarise(mean=mean(value),
            lower=quantile(value, 0.025),
            upper=quantile(value, 0.975)) %>%
  filter(facility %in% tsplotwells)

# experimental EMA time series
ewma_fit = as.data.frame(outmatrix) %>%
  select(contains("mu_ema")) %>%
  gather() %>%
  mutate(date_numeric = as.numeric(str_extract(key, "(?<=\\[)(.*?)(?=,)")) +
           min(dry_df$date_numeric) - 1,
         facility = names(ids)[as.numeric(str_extract(key, "(?<=,)(.*?)(?=\\])"))]) %>%
  select(facility, date_numeric, value) %>%
  group_by(facility, date_numeric) %>%
  summarise(mean=mean(value),
            lower=quantile(value, 0.025),
            upper=quantile(value, 0.975)) %>%
  filter(facility %in% tsplotwells)

# find plot limits
tsmax = max(c(ts_fit$upper, ar_fit$upper, ewma_fit$upper))

lintsplot = ggplot(ts_fit, aes(x=date_numeric, color=well, fill=well)) +
  geom_line(aes(y=mean), linetype="dashed") +
  geom_ribbon(aes(ymin=lower, ymax=upper), color=NA, alpha=0.25) +
  geom_line(data=tsplotdata, aes(y=mf)) +
  geom_vline(aes(xintercept = max(tsplotdata$date_numeric)), 
             linetype="dashed", color="red") +
  coord_cartesian(ylim=c(0, 60)) +
  labs(title=paste("Linear Time Series Regression for Selected Wells in PI"), 
       x="Days since baseline (2000)", linetype="")# +
  # ggsave('../_media/dry_time_series.png', width=24.7, height=8, units='cm')
ggplotly(lintsplot)

Figure 5.12: Linear regression.

saveWidget(ggplotly(lintsplot), "lintsplot.html")

arplot = ggplot(ar_fit %>% filter(facility %in% tsplotwells), 
                aes(x=date_numeric, y=mean, fill=facility, color=facility)) +
  geom_line(data=tsplotdata, aes(y=mf)) +
  geom_ribbon(aes(ymin=lower, ymax=upper), color=NA, alpha=0.5) +
  geom_line(linetype="dashed") + coord_cartesian(ylim=c(0, 60)) +
  geom_vline(aes(xintercept = max(tsplotdata$date_numeric)), 
             linetype="dashed", color="red") +
  labs(title="AR(1) Experiment", x="Days since first date", y="Mass flow (T/h)")# +
  # ggsave('../_media/ar_experiment.png', width=24.7, height=8, units='cm')
ggplotly(arplot)

Figure 5.13: First-order autoregressive model.

ewmaplot = ggplot(ewma_fit, aes(x=date_numeric, y=mean, fill=facility, color=facility)) +
  geom_line(data=tsplotdata, aes(y=mf)) +
  geom_ribbon(aes(ymin=lower, ymax=upper), color=NA, alpha=0.5) +
  geom_line(linetype="dashed") + coord_cartesian(ylim=c(0, 60)) +
  geom_vline(aes(xintercept = max(tsplotdata$date_numeric)), 
             linetype="dashed", color="red") +
  labs(title="EWMA Experiment", x="Days since first date")# +
  # ggsave('../_media/ewma_experiment.png', width=24.7, height=8, units='cm')
ggplotly(ewmaplot)

Figure 5.14: Exponentially-weighted moving average model.

We use the linear time series regression (top) for its robustness to systematic changes in operation, which can cause the other regressions to display unstable behaviour. Auto-regression and exponentially-weighted moving average techniques both have their strengths and weaknesses.

5.6.4 Goodness of fit (OLS regression)

liq_fit = as.data.frame(outmatrix) %>%
  select(contains('mf_fit')) %>%
  gather(key='index', value='fitted') %>%
  mutate(index=as.integer(parse_number(index))) %>%
  group_by(index) %>%
  summarise(lower=quantile(fitted, 0.025),
            upper=quantile(fitted, 0.975),
            Fitted=mean(fitted),
            std=sd(fitted)) %>%
  cbind(regression_df) %>%
  mutate(`Standardised residual` = (Fitted-mf)/std,
         Well = factor(names(ids[well_id])),
         Observed = mf) %>%
  gather(key="key", value="value", `Standardised residual`, Observed) %>%
  select(Well, key, Fitted, value, source)

diagplot = ggplot(liq_fit, aes(x=Fitted, y=value)) +
  geom_point(aes(color=Well, shape=Well)) + 
  scale_shape_manual(values = rep_len(1:25, length(unique(liq_fit$Well)))) +
  geom_smooth(color='black') +
  facet_wrap(~key, scales="free") +
  geom_hline(data=data.frame(key="Standardised residual", value=c(1.96,-1.96)),
             aes(yintercept=value), color='red') +
  geom_abline(data=data.frame(key="Observed", a = 1, b = 0),
              aes(slope = a, intercept=b), color='red') +
  # coord_cartesian(ylim=c(-4, 4)) +
  labs(title="Diagnostic Plots", x="Fitted mass flow (T/h)", y="") +
  theme(legend.position = "bottom") +
  guides(color=guide_legend(nrow=3, byrow=T), shape=guide_legend(nrow=3, byrow=T))# +
  # ggsave('../_media/diagnostics.png', width=24.7, height=12, units='cm')
diagplot

## `geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'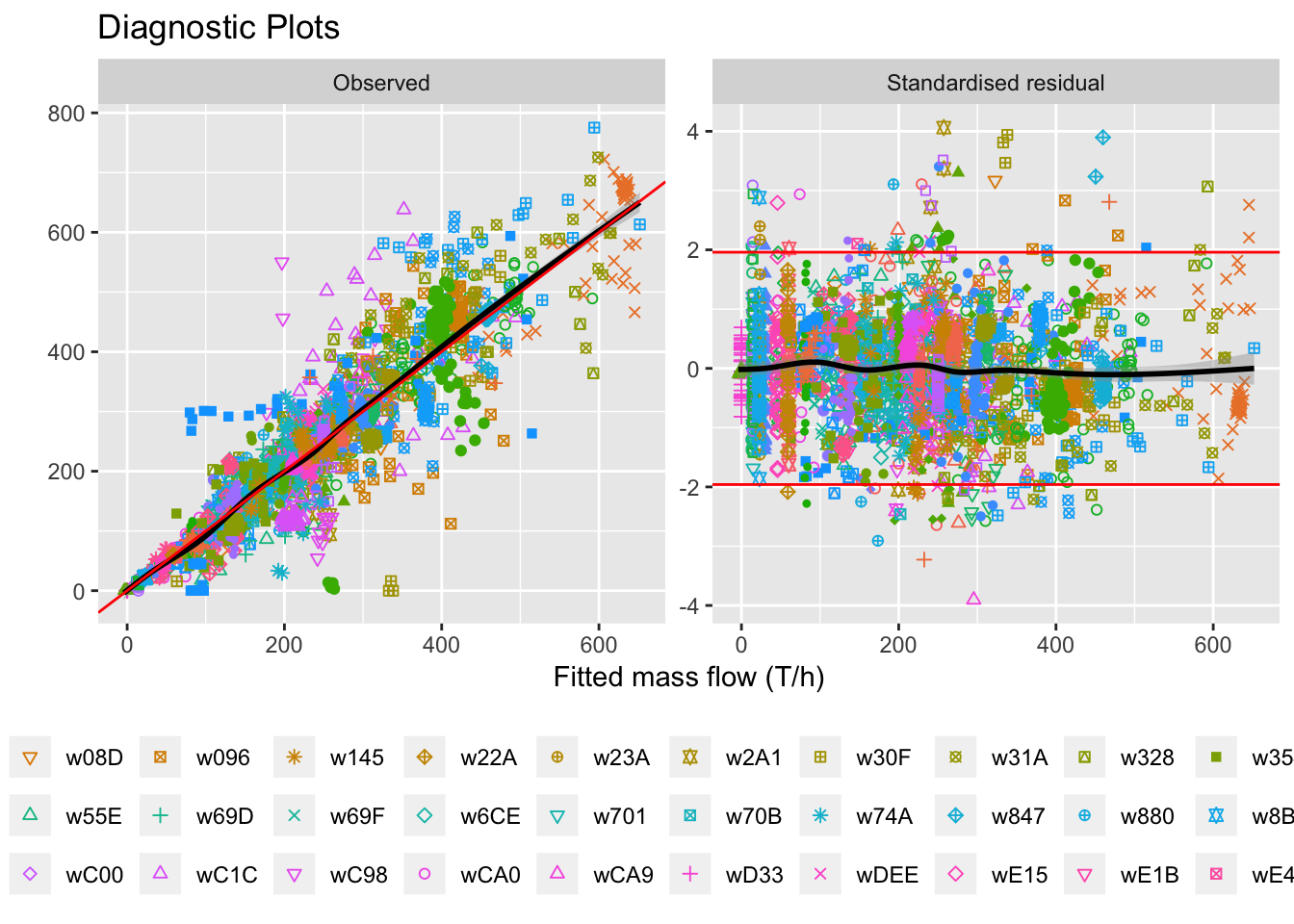

Figure 5.15: Diagnostic plots with all wells together.

selectwells = liq_fit %>% group_by(Well, key) %>%
  summarise(fittedsd = sd(Fitted)) %>%
  arrange(desc(fittedsd)) %>%
  head(48*2) %>%
  pull(Well)

observedplot = ggplot(liq_fit %>% filter(key=="Observed", Well %in% selectwells),
                      aes(x=Fitted, y=value)) +
  geom_point(aes(color=source), alpha=0.5) +
  geom_smooth(color=NA, alpha=0.5) +
  facet_wrap(~Well, scales="free") +
  geom_abline(data=data.frame(key="Observed", a = 1, b = 0),
              aes(slope = a, intercept=b)) +
  labs(title="Linear Regression Fit Plots Per Well",
       x="Fitted mass flow (T/h)", y="Observed mass flow (T/h)", color="Data source") +
  theme(legend.position = "bottom")# +
  # guides(color=guide_legend(nrow=3, byrow=T), shape=guide_legend(nrow=3, byrow=T)) +
  # ggsave('../_media/observed.png', width=24.7, height=24.7, units='cm')
observedplot

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'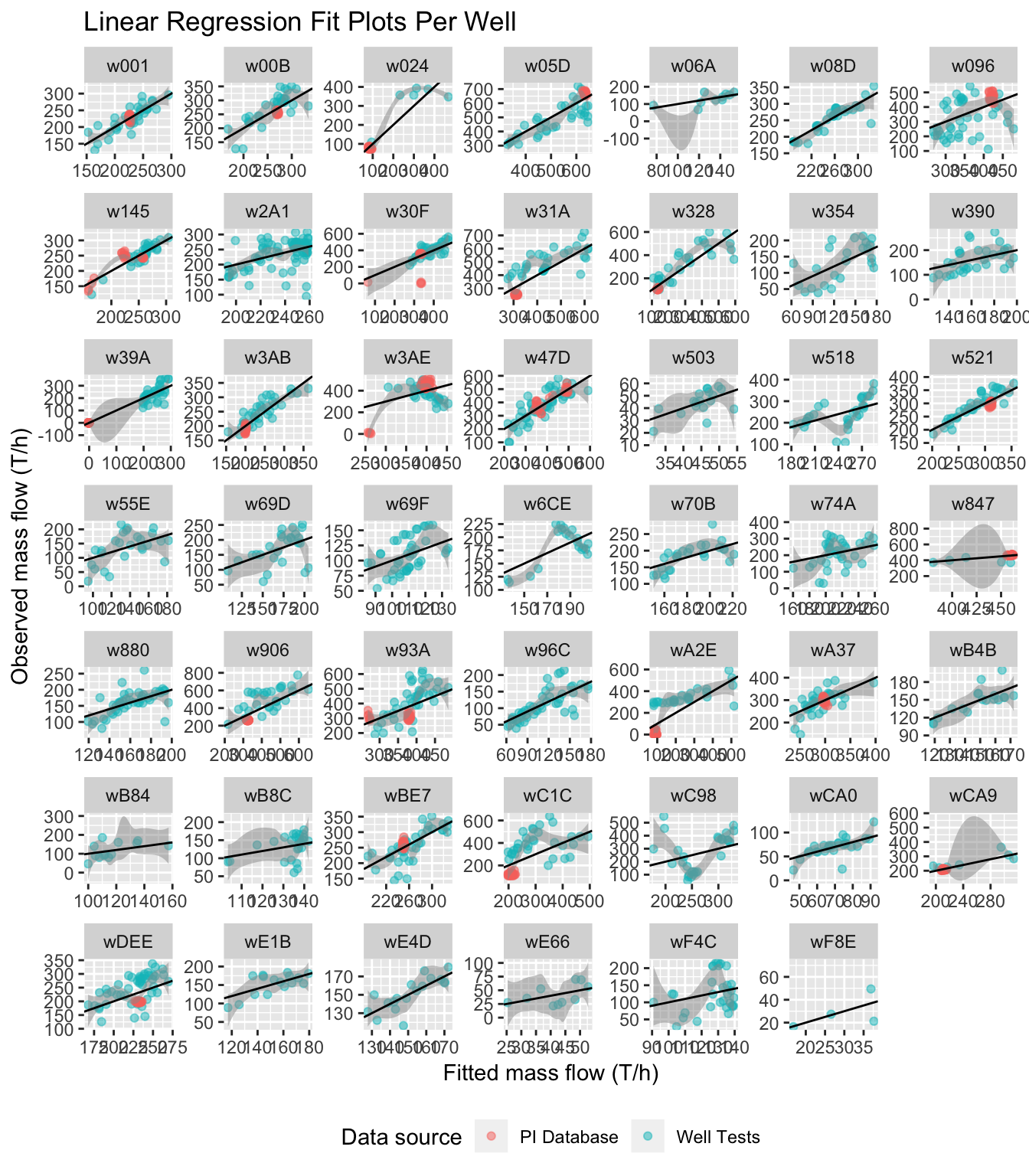

Figure 5.16: Observed vs. fitted for individual wells

stdresplot = ggplot(liq_fit %>% filter(key=="Standardised residual",
                                       Well %in% selectwells),
                    aes(x=Fitted, y=value)) +
  geom_point(aes(color=source), alpha=0.5) +
  geom_smooth(color=NA, alpha=0.5) +
  facet_wrap(~Well, scales="free_x") +
  geom_hline(data=data.frame(key="Standardised residual", value=c(1.96,-1.96)),
             aes(yintercept=value), color='red') +
  # geom_abline(data=data.frame(key="Observed", a = 1, b = 0), aes(slope = a, intercept=b), color='red') +
  labs(title="Linear Regression Residual Plots Per Well",
       x="Fitted mass flow (T/h)", y="Standardised residual", color="Data source") +
  coord_cartesian(ylim=c(-5, 5)) +
  theme(legend.position="bottom",
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())# +
  # guides(color=guide_legend(nrow=3, byrow=T), shape=guide_legend(nrow=3, byrow=T)) +
  # ggsave('../media/stdres_sans.png', width=18, height=12, units='cm')
stdresplot

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'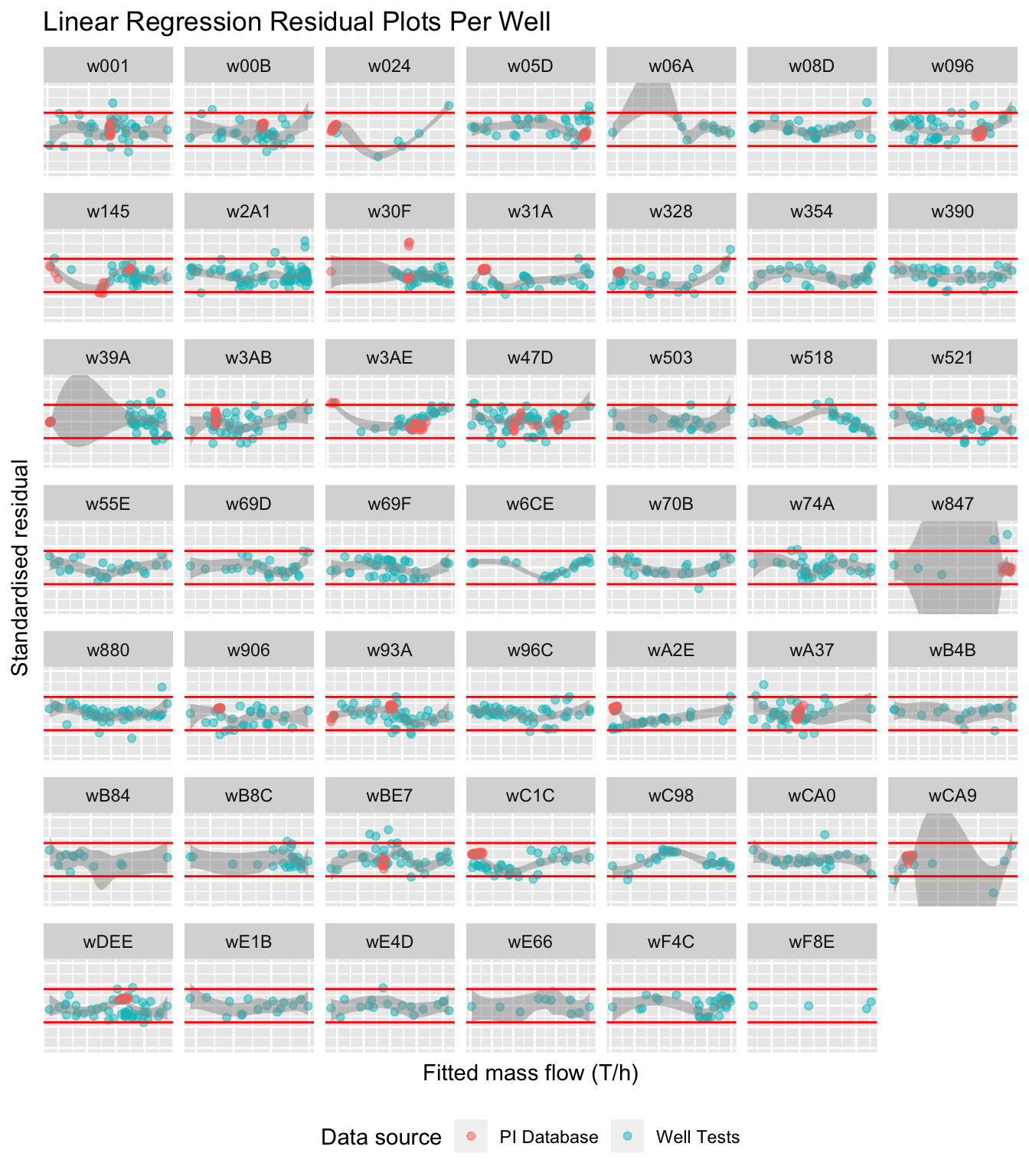

Figure 5.17: Standardised residuals for individual wells

5.6.5 Limits and Constraint Violations

sf.df <- outframe %>% 
  filter(str_detect(variable, "total_sf") & value > 0) %>% 
  droplevels()
limits = fp_constants %>%
  mutate(facility = names(ids)[fp_id]) %>%
  select(facility, limit) %>% 
  drop_na()

p.limits = sf.df %>%
  left_join(limits, by=c("facility")) %>%
  mutate(greater = value > limit) %>%
  group_by(facility) %>%
  summarise(p.greater = mean(greater)) %>%
  drop_na()

limitplot = ggplot(sf.df %>% filter(facility %ni% incomplete.fps),
                   aes(x=value, fill=facility)) +
  facet_wrap(~facility, scales = "free_y", ncol=2) +
  geom_density(alpha=0.5, color=NA) +
  geom_vline(data=limits, aes(xintercept=limit), color="red") +
  geom_label(data=p.limits %>% filter(facility %ni% incomplete.fps),
             aes(x=-Inf, y=Inf, hjust=0, vjust=1,
                 label=paste0("p(>lim)=", p.greater), family="Times New Roman"),
             color="black", label.size=0, fill='white') +
  theme(legend.position="none",
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  labs(title="Posterior Flash Plant Mass Flows",
       x="Steam flow (T/h)", y="Density", fill="Flash plant", color="Steam flow limit")# +
  # ggsave('../_media/constraints.png', width=24.7, height=10, units='cm')
limitplot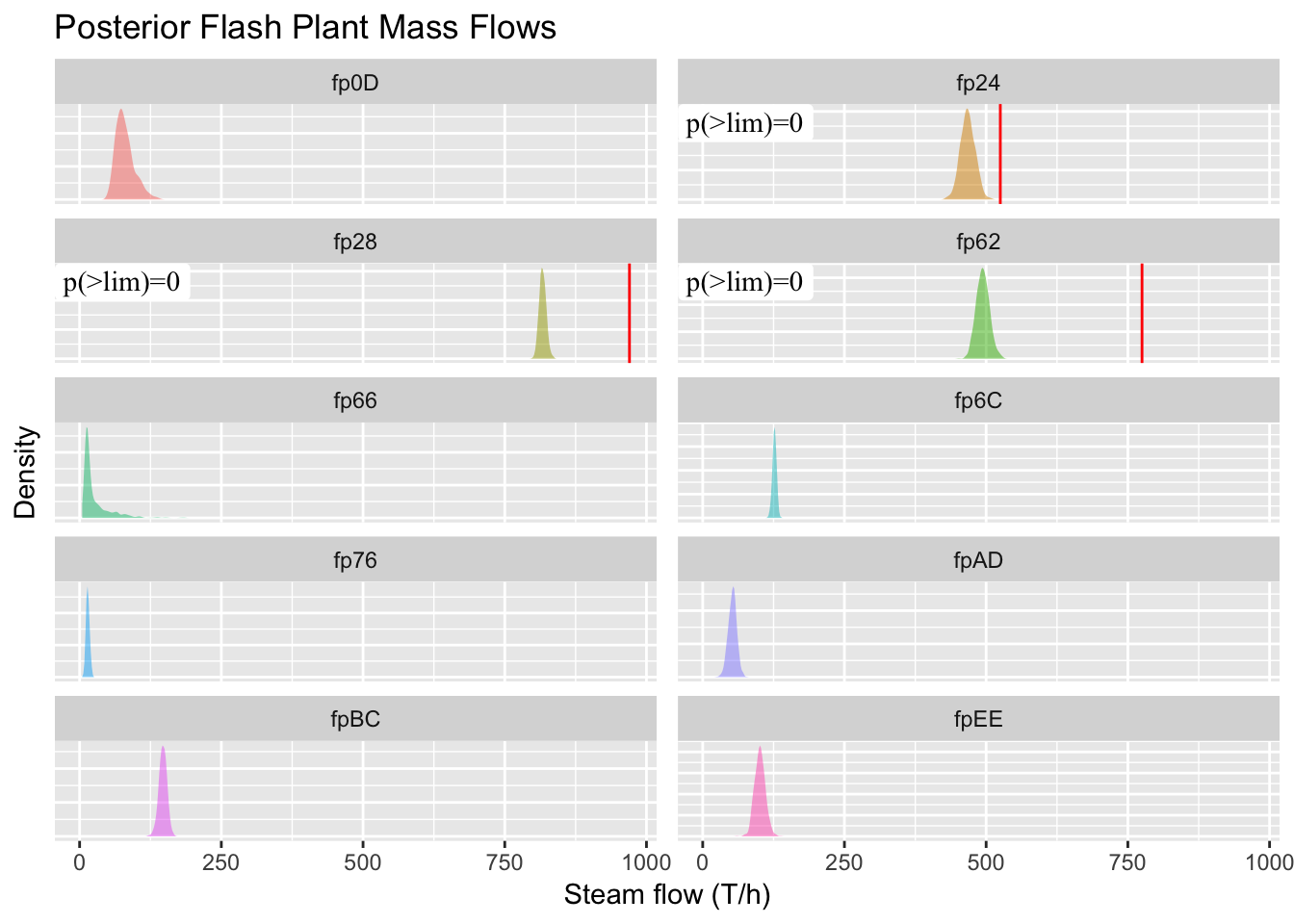

Figure 5.18: We expect the curves to make better predictions near the PI data after inclusion. Forecasted production curves for December 1st, and shaded regions are 95% credible intervals.

The following plot is for the presentation, focusing on the three FPs that feed from configurable wells.

sf.df2 <- sf.df %>%
  filter(facility %in% p.limits$facility)
limitplot2 = ggplot(sf.df2, aes(x=value, fill=facility)) +
  facet_wrap(~facility, scales = "free_y", ncol=1) +
  geom_density(alpha=0.5, color=NA) +
  geom_vline(data=limits, aes(xintercept=limit), color="red") +
  # geom_label(data=p.limits %>% filter(facility %ni% incomplete.fps),
  #            aes(x=-Inf, y=Inf, hjust=0, vjust=1,
  #                label=paste0("p(>lim)=", p.greater), family="Times New Roman"),
  #            color="black", label.size=0, fill='white') +
  xlim(0, NA) +
  theme(legend.position="none",
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank()) +
  labs(title="Posterior Flash Plant Mass Flows",
       x="Steam flow (T/h)", y="Density", fill="Flash plant", color="Steam flow limit")# +
  # ggsave('../media/constraints2.png', width=16, height=9, units='cm')
ggplotly(limitplot2)

Figure 5.19: Limit comparison for three FPs with flow limits.

saveWidget(ggplotly(limitplot2), "limitplot.html")

5.6.6 Flow Comparison

flow.df <- outframe %>% 
  filter(facility %in% fp_names) %>%
  filter(str_detect(variable, "mf_pred|ip_sf|lp_sf|wf") & value > 0) %>%
  mutate(variable=ifelse(variable=="mf_pred", "mf", variable),
         variable=factor(variable, levels=c("mf", "ip_sf", "lp_sf", "wf")))

comparison = fp_constants %>% select("fp", contains("verification")) %>%
  rename(facility=fp) %>%
  gather(key="variable", value="value", -facility) %>%
  mutate(variable = gsub("^verification_", "", variable),
         variable=factor(variable, levels=c("mf", "ip_sf", "lp_sf", "wf"))) %>%
  drop_na()

ps = flow.df %>%
  left_join(comparison, by=c("facility", "variable")) %>%
  mutate(greater = value.x > value.y) %>%
  group_by(facility, variable) %>%
  summarise(p.greater = mean(greater)) %>%
  mutate(variable=factor(variable, levels=c("mf", "ip_sf", "lp_sf", "wf"))) %>%
  drop_na()

verificationplot = ggplot(flow.df %>% filter(facility %ni% incomplete.fps,
                                             variable %in% c("mf", "lp_sf", "wf")),
                          aes(x=value)) +
  geom_density(aes(y=..scaled.., fill=variable, color=variable),
               alpha=0.5, show.legend=F) +
  geom_vline(data=comparison %>% filter(facility %ni% incomplete.fps,
                                        variable %in% c("mf", "lp_sf", "wf")),
             aes(xintercept=value)) +
  # geom_label(data=ps %>% filter(facility %ni% incomplete.fps),
  #            aes(x=-Inf, y=Inf, hjust=0, vjust=1, label=paste0("p(>x)=", p.greater),
  #                family="Times New Roman"), label.size=0) +
  facet_grid(facility~variable, scales="free", space="free_y") +
  theme(axis.text.y=element_blank(), axis.ticks.y=element_blank()) +
  labs(title="Comparison Between Predicted FP Flows and Sample Data",
       x="Value", y="Scaled density")# +
  # ggsave('../media/verification_sans.png', width=18, height=12, units='cm')
verificationplot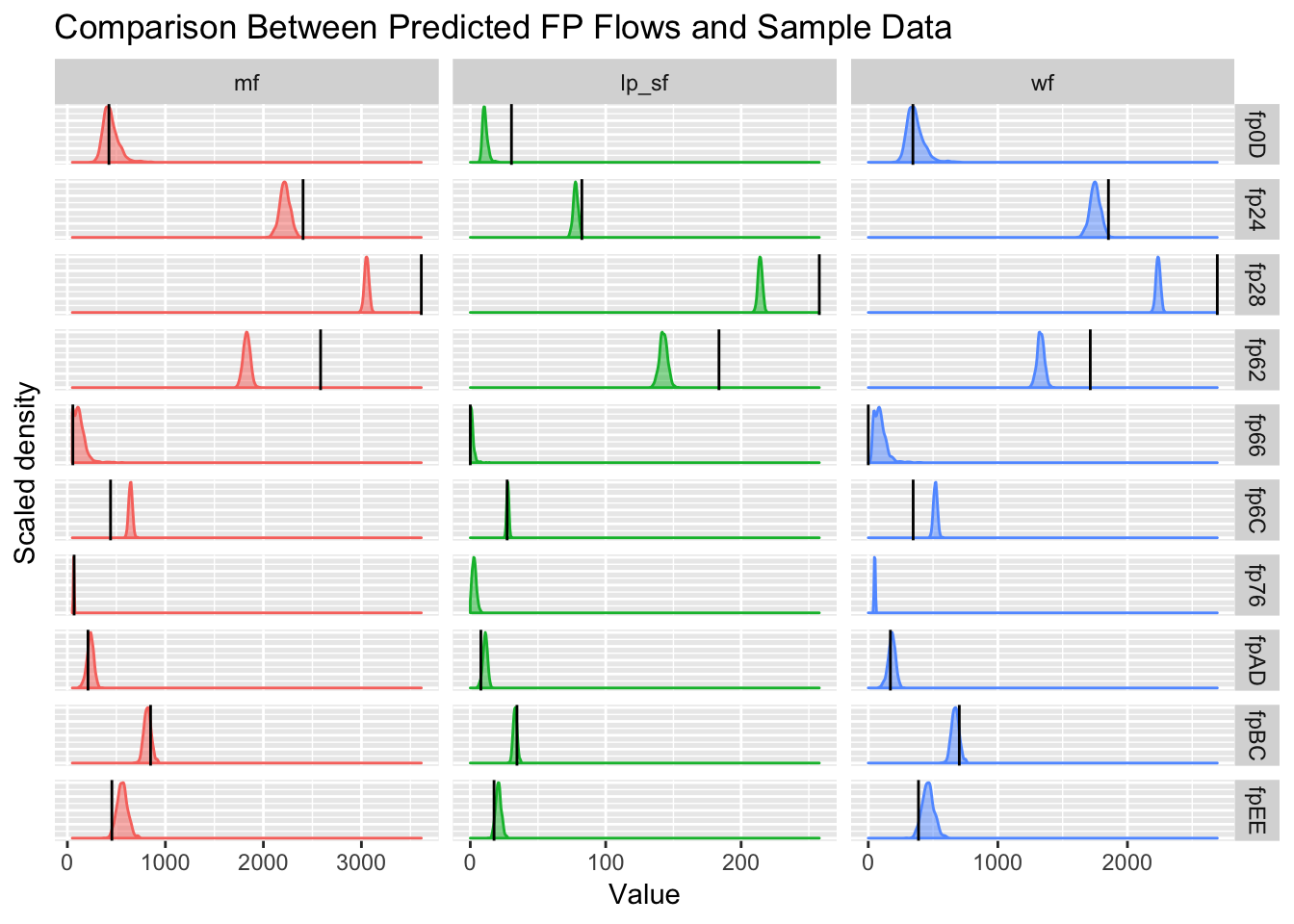

Figure 5.20: Verification of predicted flows with supplied calculations shows some disagreement (\(p<0.025\) or \(p>0.975\)), if we assume CEL’s figures as the ground truth. Densities are the model’s forecasts and black lines are the given figures from CEL (estimated by CEL, not direct from the PI loggers).